2.2.3 Drawing filled triangles | JAVA 3D Programming | Chapter 2

2.2.3 Drawing filled triangles

Java 3D rendered the hand as an apparently solid object. We cannot see the triangles that compose the hand, and triangles closer to the viewer obscure the triangles further away.

       

You could implement similar functionality within MyJava3D in several ways:

Hidden surface removal

You could calculate which triangles are not visible and exclude them from rendering. This is typically performed by enforcing a winding order on the vertices that compose a triangle. Usually vertices are connected in a clockwise order. This allows the graphics engine to calculate a vector that is normal (perpendicular) to the face of the triangle. The triangle will not be displayed if its normal vector is pointing away from the viewer.

This technique operates in object space—as it involves mathematical operations on the objects, faces, and edges of the 3D objects in the scene. It typically has a computational complexity of order n2 where n is the number of faces.

This quickly becomes complicated however as some triangles may be partially visible. For partially visible triangles, an input triangle has to be broken down into several new wholly visible triangles. There are many good online graphics courses that explain various hidden−surface removal algorithms in detail. Use your favorite search engine and search on “hidden surface removal” and you will find lots of useful references.

Depth sorting (Painter’s algorithm)

The so−called Painter’s algorithm also operates in object space; however, it takes a slightly different approach. The University of North Carolina at Chapel Hill Computer Science Department online course Introduction to Computer Graphics (http://www.cs.unc.edu/~davemc/Class/136/) explains the Painter’s algorithm (http://www.cs.unc.edu/~davemc/Class/136/Lecture19/Painter.html)

The basic approach for the Painter’s algorithm is to sort the triangles in the scene by their distance from the viewer. The triangles are then rendered in order: triangle furthest away rendered first, closest triangle rendered last. This ensures that the closer triangles will overlap and obscure triangles that are further away.

        An uncomplicated depth sort is easy to implement; however, once you start using it you will begin to see strange rendering artifacts. The essential problem comes down to how you measure the distance a triangle is from the viewer. Perhaps you would:

• Take the average distance of each of the three vertices

• Take the distance of the centroid of the triangle

With either of these simple techniques, you can generate scenes with configurations of triangles that render incorrectly. Typically, problems occur when:

• Triangles intersect

• Centroid or average depth of the triangle is not representative of the depth of the corners

• Complex shapes intersect

• Shapes require splitting to render correctly

For example, figure 2.5 shows some complex configurations of triangles that cannot be depth sorted using a simple algorithm.

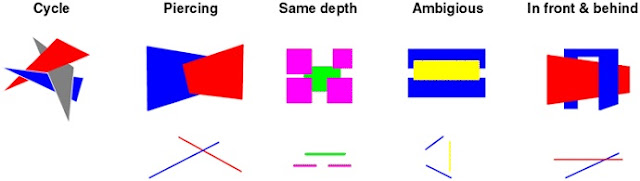Figure 2.5 Interesting configurations of triangles that are challenging for depth−sorting algorithms

The depth of an object in the scene can be calculated if the position of the object is known and the position of the viewer or image plane is known. It would be computationally intensive to have to re−sort all the triangles in the scene every time an object or the viewer’s position changed. Fortunately, binary space partition (BSP) trees can be used to store the relative positions of the object in the scene such that they do not need to be re−sorted when the viewpoint changes. BSP trees can also help with some of the complex sorting configurations shown earlier.

Depth buffer (Z−buffer)

In contrast to the other two algorithms, the Z−buffer technique operates in image space. This is conceptually the simplest technique and is most commonly implemented within the hardware of 3D graphics cards.

If you were rendering at 640 × 480 resolution, you would also allocate a multidimensional array of integers of size 640 × 480. The array (called the depth buffer or Z−buffer) stores the depth of the closest pixel rendered into the image.

As you render each triangle in your scene, you will be drawing pixels into the frame−buffer. Each pixel has a color, and an xy−coordinate in image space. You would also calculate the z−coordinate for the pixel and update the Z−buffer. The values in the Z−buffer are the distance of each pixel in the frame from the viewer.

Before actually rendering a pixel into the frame−buffer for the screen display, inspect the Z−buffer and notice whether a pixel had already been rendered at the location that was closer to the viewer than the current pixel. If the value in the Z−buffer is less than the current pixel’s distance from the viewer, the pixel should be obscured by the closer pixel and you can skip drawing it into the frame−buffer.

It should be clear that this algorithm is fairly easy to implement, as long as you are rendering at pixel level; and if you can calculate the distance of a pixel from the viewer, things are pretty straightforward. This algorithm also has other desirable qualities: it can cope with complex intersecting shapes and it doesn’t need to split triangles. The depth testing is performed at the pixel level, and is essentially a filter that prevents some pixel rendering operations from taking place, as they have already been obscured.

The computational complexity of the algorithm is also far more manageable and it scales much better with large numbers of objects in the scene. To its detriment, the algorithm is very memory hungry: when rendering at 1024 × 800 and using 32−bit values for each Z−buffer entry, the amount of memory required is 6.25 MB.

The memory requirement is becoming less problematic, however, with newer video cards (such as the nVidia Geforce II/III) shipping with 64 MB of memory.

The Z−buffer is susceptible to problems associated with loss of precision. This is a fairly complex topic, but essentially there is a finite precision to the Z−buffer. Many video cards also use 16−bit Z−buffer entries to conserve memory on the video card, further exacerbating the problem. A 16−bit value can represent 65,536 values—so essentially there are 65,536 depth buckets into which each pixel may be placed. Now imagine a scene where the closest object is 2 meters away and the furthest object is 100,000 meters away. Suddenly only having 65,536 depth values does not seem so attractive. Some pixels that are really at different distances are going to be placed into the same bucket. The precision of the Z−buffer then starts to become a problem and entries that should have been obscured could become randomly rendered. Thirty−two−bit Z−buffer entries will obviously help matters (4,294,967,296 entries), but greater precision merely shifts the problem out a little further. In addition, precision within the Z−buffer is not uniform as described here; there is greater precision toward the front of the scene and less precision toward the rear.

When rendering using a Z−buffer, the rendering system typically requires that you specify a near and a far clipping plane. If the near clipping plane is located at z = 2 and the far plane is located at z = 10, then only objects that are between 2 and 10 meters from the viewer will get rendered. A 16−bit Z−buffer would then be quantized into 65,536 values placed between 2 and 10 meters. This would give you very high precision and would be fine for most applications. If the far plane were moved out to z = 50,000 meters then you will start to run into precision problems, particularly at the back of the visible region.

In general, the ratio between the far and near clipping (far/near) planes should be kept to below 1,000 to avoid loss of precision. You can read a detailed description of the precision issues with the OpenGL depth buffer at the OpenGL FAQ and Troubleshooting Guide (http://www.frii.com/~martz/oglfaq/depthbuffer.htm).